The complex plane (or the Argand plane) is a representation of the complex numbers established by the real axis (horizontal) and the imaginary axis (vertical). It can be thought of as a Cartesian plane, where you plot \(\text{Re}(z)\) on the \(x\)-axis and \(\text{Im}(z)\) on the \(y\)-axis.
Worked example: Plot \(z_1 = 3+2i\) and \(z_2=3-2i\) on the complex plane.
Solution: This is equivalent to plotting \((3,2)\) and \((3,-2)\) on a Cartesian plane.
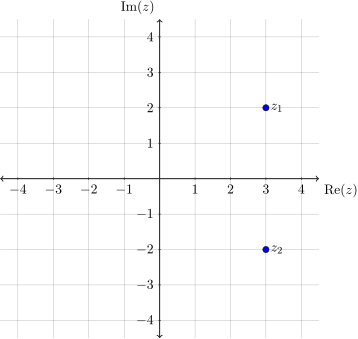
Notice that \(z_2\) is a reflection of \(z_1\) on the imaginary axis, as they are conjugates.
Problems
- Plot the following complex numbers on the complex plane.
- \(3+4i\)
- \(-3-4i\)
- \(i\)
- \(1-i\)
- \( \frac{1}{2}-\frac{3}{2}i\)
- \(9i-1\)
- Let \(z = 2+i\). Sketch carefully on the same Argand diagram.
- \(z\)
- \(-z\)
- \(\overline{z}\)
- \(-2z\)
- \(iz\)
- What is the relationship between \(z\), \(-z\) and \(\overline{z}\) on the complex plane?