Recall that adding complex numbers simply involves adding the real parts and imaginary parts separately. When represented as vectors on the complex plane, this is the same as adding vectors “tip to tail” and forming a parallelogram.
Example. To add the complex numbers \(2-i\) and \(1+3i\) we draw the vectors tip to tail. It doesn’t matter which order you add the vectors, the result is still \(3+2i\). Geometrically, the addition of two vectors forms a parallelogram.
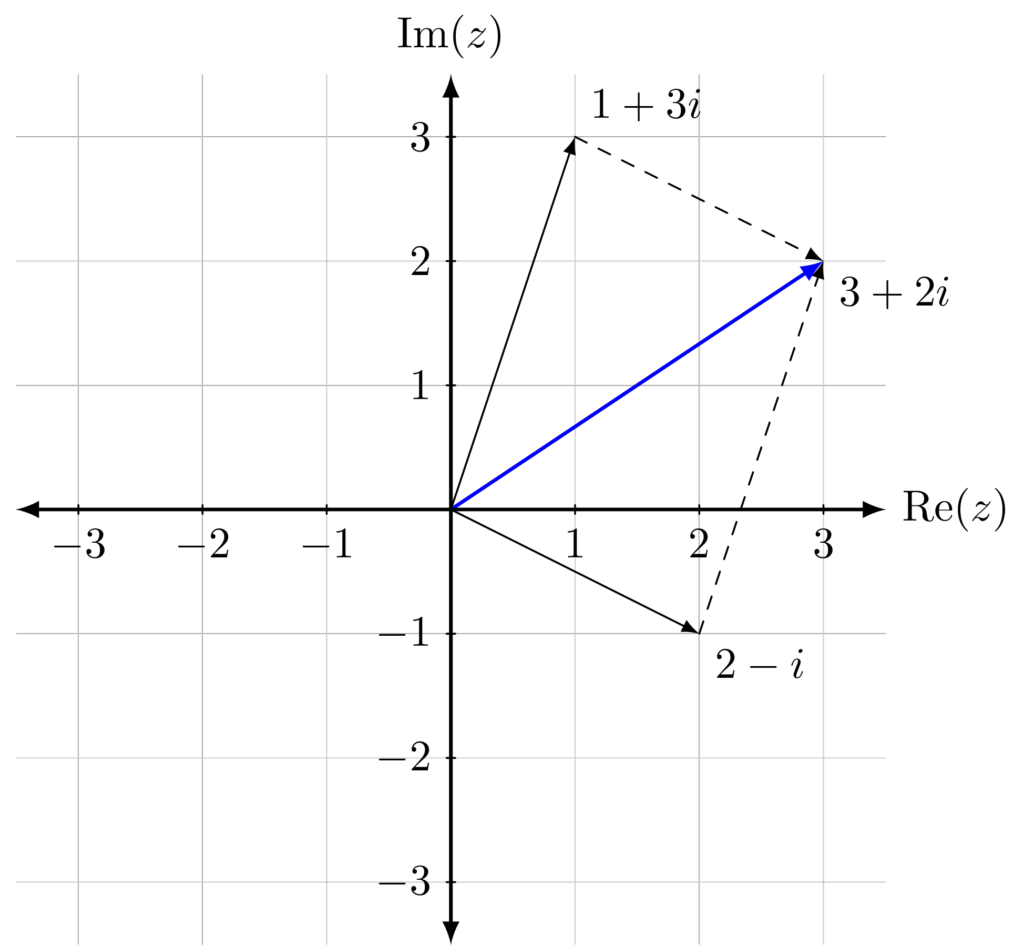
It is often easier to write out vector additions in arrow notation, where a vector from point \(A\) to point \(B\) is written as \(\overrightarrow{AB}\).
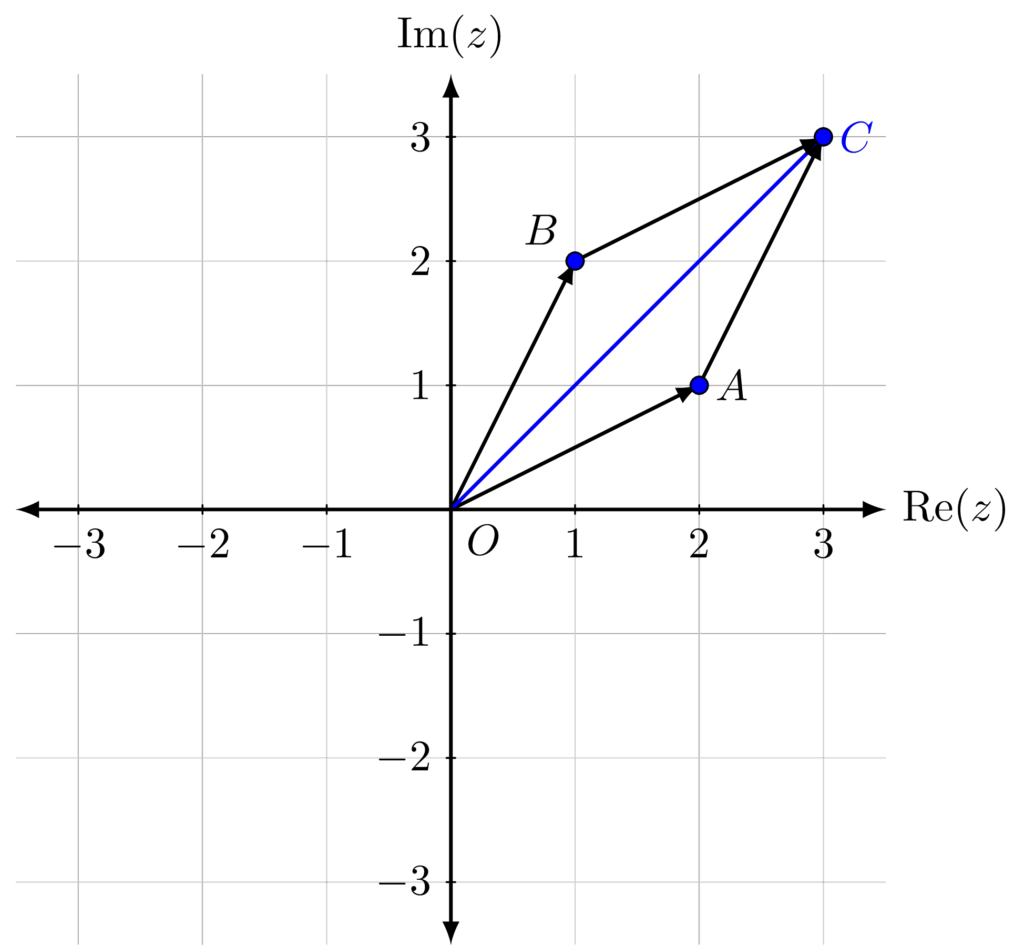
Example. Let \(z=2+i\) and \(w=1+2i\). Let \(A\), \(B\) and \(C\) be the points representing \(z\), \(w\) and \(z+w\) respectively. Let \(O\) represent the origin. Then the point representing \(z+w\) is represented by the vector \(\overrightarrow{OC}\), and $$\begin{align*}
\overrightarrow{OC} &= \overrightarrow{OA}+\overrightarrow{AC} \\
&=\overrightarrow{OA}+\overrightarrow{OB} \\
&= (2+i)+(1+2i) = 3+3i \end{align*}$$
Problems
- Add the following complex numbers as vectors on the complex plane.
- \(1+i\) and \(2+i\)
- \(-1-2i\) and \(5-i\)
- Let \(z_1\), \(z_2\) and \(z_3\) be complex numbers, represented by the points \(A\), \(B\) and \(C\) on the complex plane. Let \(O\) be the origin. What are the conditions required on \(z_1\), \(z_2\) and \(z_3\) for \(OABC\) to be a parallelogram? What about a rhombus?