Definition. An argument of a complex number \(z\), denoted as \( \arg (z) \), is defined as the angle inclined (measured counterclockwise) from the positive real axis in the direction of the complex number represented on the complex plane. The argument is usually expressed in radians.

The argument of the complex number \(0\) is undefined.
Any non-zero complex number can have multiple arguments, as arguments differing by an integer multiple of \(2\pi\) are the same.

Because of this, we define the principal argument of a complex number.
Definition. The principal argument of a complex number \(z\), denoted as \( \text{Arg}(z)\) (with a capital A), is the unique argument of \(z\) such that $$ – \pi < \text{Arg}(z) \le \pi.$$
Worked example. Find the principal argument of \(\sqrt{3}-i\).
Solution. Plotting \(\sqrt{3}-i\) on the complex plane, we have the following.
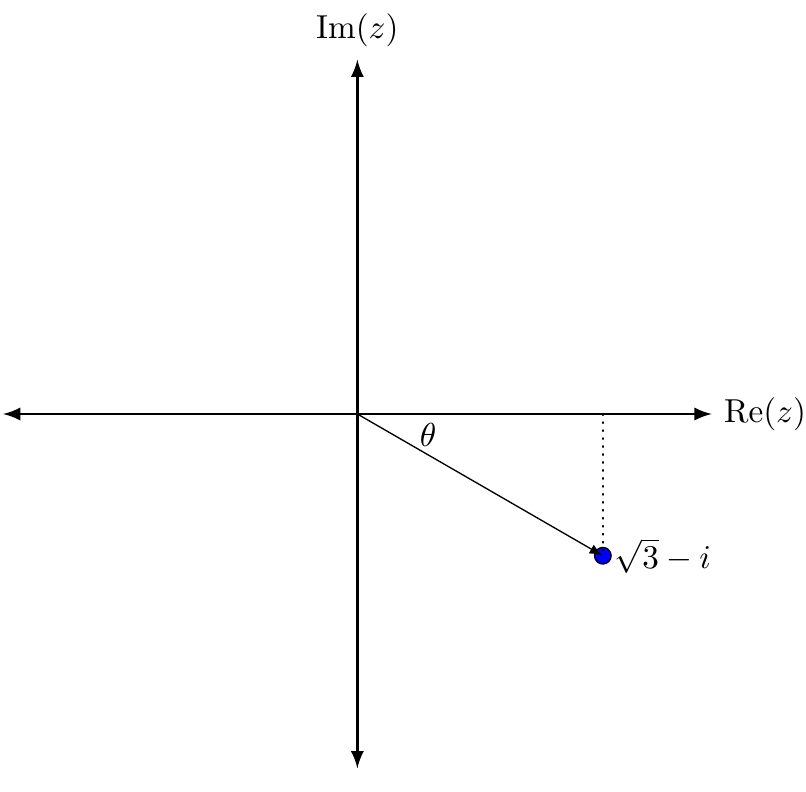
We can see that we form a right-angled triangle with width \(\sqrt{3}\) and height \(1\), and using trigonometry we can see that \( \theta = \frac{\pi}{6}\). Hence, \( \text{Arg}(\sqrt{3}-i) = – \frac{\pi}{6} \).
In the previous example, the other non-principal arguments are \( -\frac{\pi}{6} + 2\pi n\), where \(n\) is any integer, that is the set $$\{ \dots, -\frac{25\pi}{6}, -\frac{13\pi}{6}, -\frac{\pi}{6}, \frac{11\pi}{6}, \frac{23\pi}{6}, \dots\}.$$
GL tip. You may be tempted to conclude that the formula for the principal argument is $$ \text{Arg} (x+yi) = \tan^{-1} \left( \frac{y}{x} \right).$$ However, this formula only holds true when \(x > 0\), because the range of the inverse tangent function is between \(-\frac{\pi}{2}\) and \(-\frac{\pi}{2}\). Instead of using a formula, it is best to draw a diagram and use trigonometry!
Problems
- Find the argument of the following complex numbers, with the answer in exact form if possible, otherwise to two significant figures.
- \(-i\)
- \(-1\)
- \(1+i\)
- \(-1-i\)
- \(100-100i\)
- \(4+3i\)
- \(-4+3i\)