Scaling and rotating complex numbers as vectors

Scaling complex numbers

When a complex number $z$ is multiplied by a positive real number, then it scales the length of the vector, keeping the same direction. If it is multiplied by a negative real number, then it reverses the direction and also scales the length.

Example. Let $z=1+i$. Then we can plot $2z$, $-3z$ and $0.5z$ as vectors.

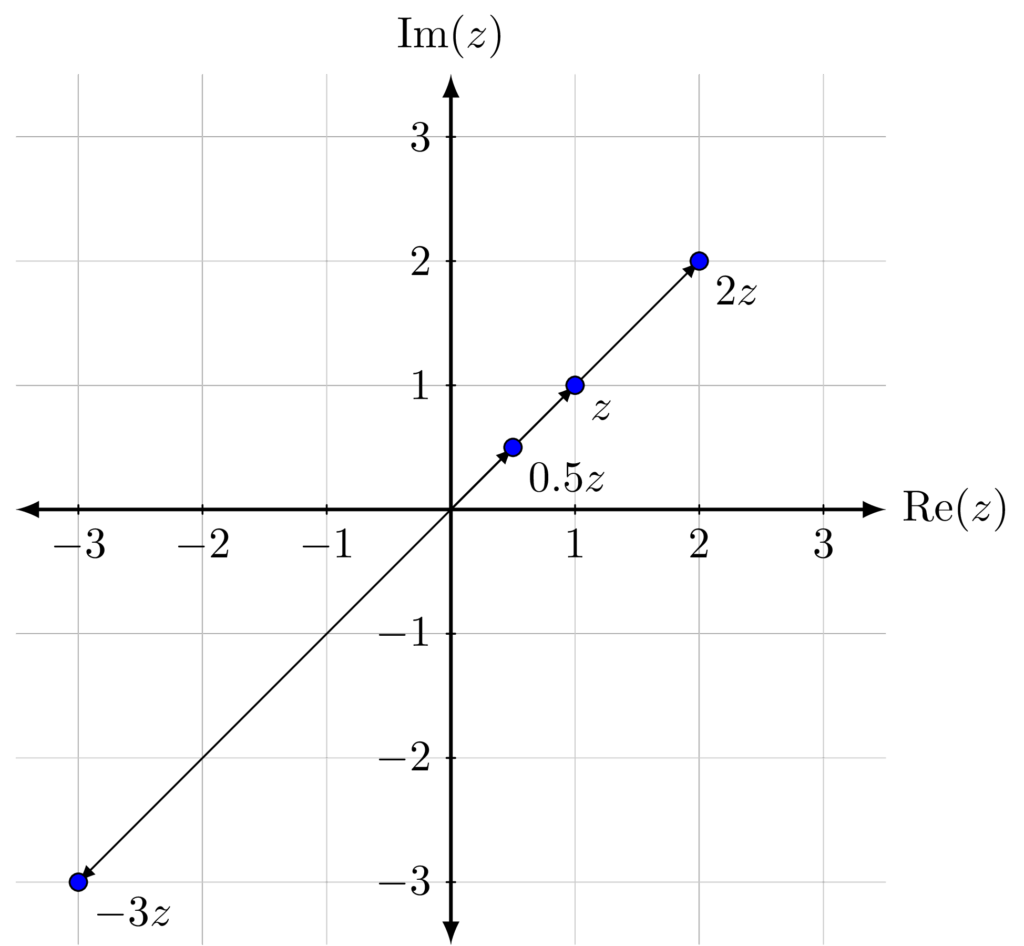
Rotating complex numbers

When a complex number $z$ is multiplied by $r(\cos\theta+i\sin\theta)$, it is rotation of $\theta$ counter-clockwise and the length is multiplied by $r$.

Similarly, when a complex number $z$ is divided by $r(\cos\theta+i\sin\theta)$, it is rotation of $\theta$ clockwise and the length is divided by $r$.

Example. When a vector is multiplied by $i$, it is a 90 degree rotation counterclockwise with no change in modulus.

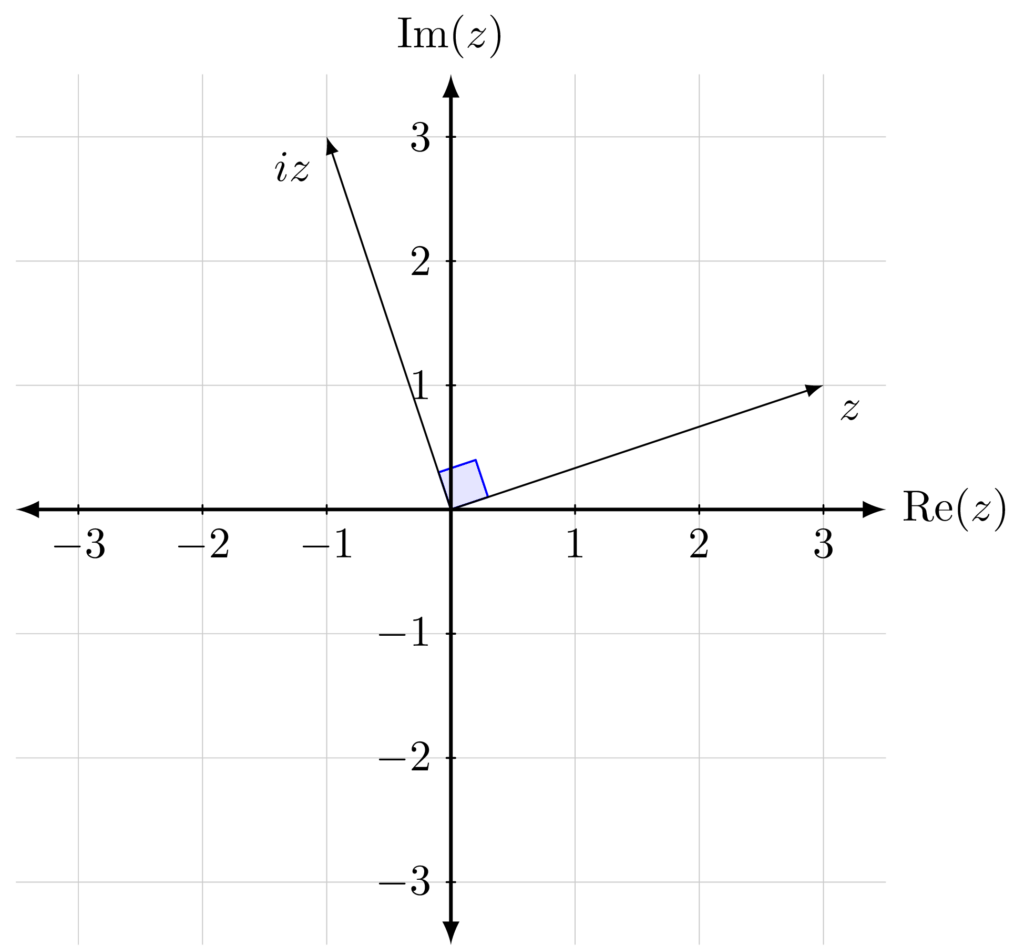
Worked exercise. Let $z=re^{i\theta}$, where $0<\theta<\frac{\pi}{2}$. Represent $z$, $-iz$, $\overline{z}$ and $(\sqrt{3}+i)z$ as vectors on the complex plane.
Solution. $-iz$ is a clockwise rotation of $z$ by 90 degrees. $\overline{z}$ is a reflection of $z$ in the real axis. $\sqrt{3}+i = 2e^{\frac{i\pi}{6}}$, so $(\sqrt{3}+i)z$ is a 30 degree rotation counter-clockwise, followed by a scaling by 2.

Problems

Let $z=1+2i$. Plot the following complex numbers as vectors on the complex plane.
1. $z$
2. $-z$
3. $\overline{z}$
4. $3z$
5. $iz$
$z_1$, $z_2$ and $z_3$ are three complex numbers such that $$z_2-z_1=i(z_3-z_1).$$ If points $P$, $Q$ and $R$ represent the complex numbers $z_1$, $z_2$ and $z_3$ respectively, what geometric properties does the triangle $PQR$ have?
Let $O$ be the point that represents the complex number $0$, and points $P$ and $Q$ represent the complex numbers $z_1$ and $z_2$ respectively. Triangle $OPQ$ is equilateral. Show that $z_1^2+z_2^2=z_1z_2$.
Hard. Let $z$ and $w$ be complex numbers such that $\frac{z-w}{z+w}$ is imaginary. Show geometrically that $|z|=|w|$.