Notice that for complex numbers \(z\) and \(w\), \(z-w=z+(-w)\). In other words, subtracting \(w\) from \(z\) is the same as adding \(-w\) to \(z\).
The representation of the negative of a vector is an arrow which points in the opposite direction with a same magnitude.

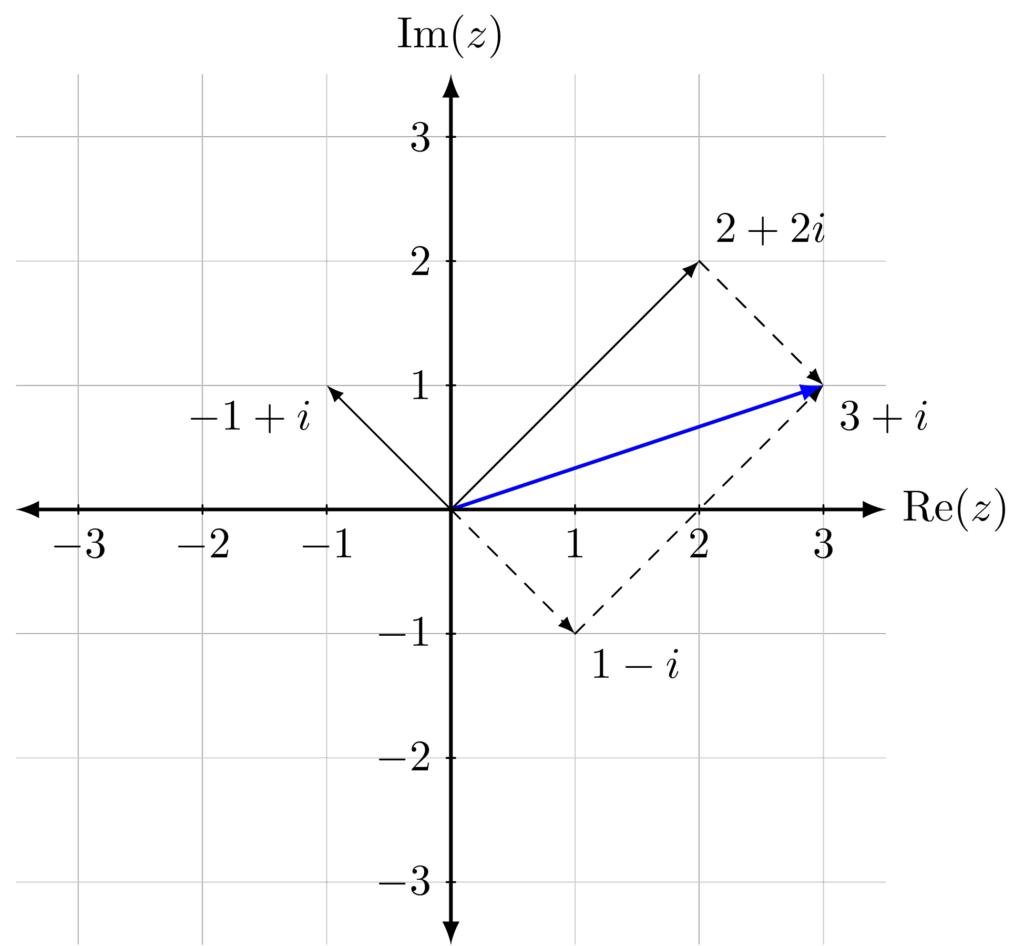
Example. Let \(z=(2+2i)\) and \(w=-1+i\). To evaluate \(z-w\), we find \(-w\), which is \(1-i\) (dashed), and then we perform the vector addition of \(z\) and \(-w\), which gives us \(3+i\).
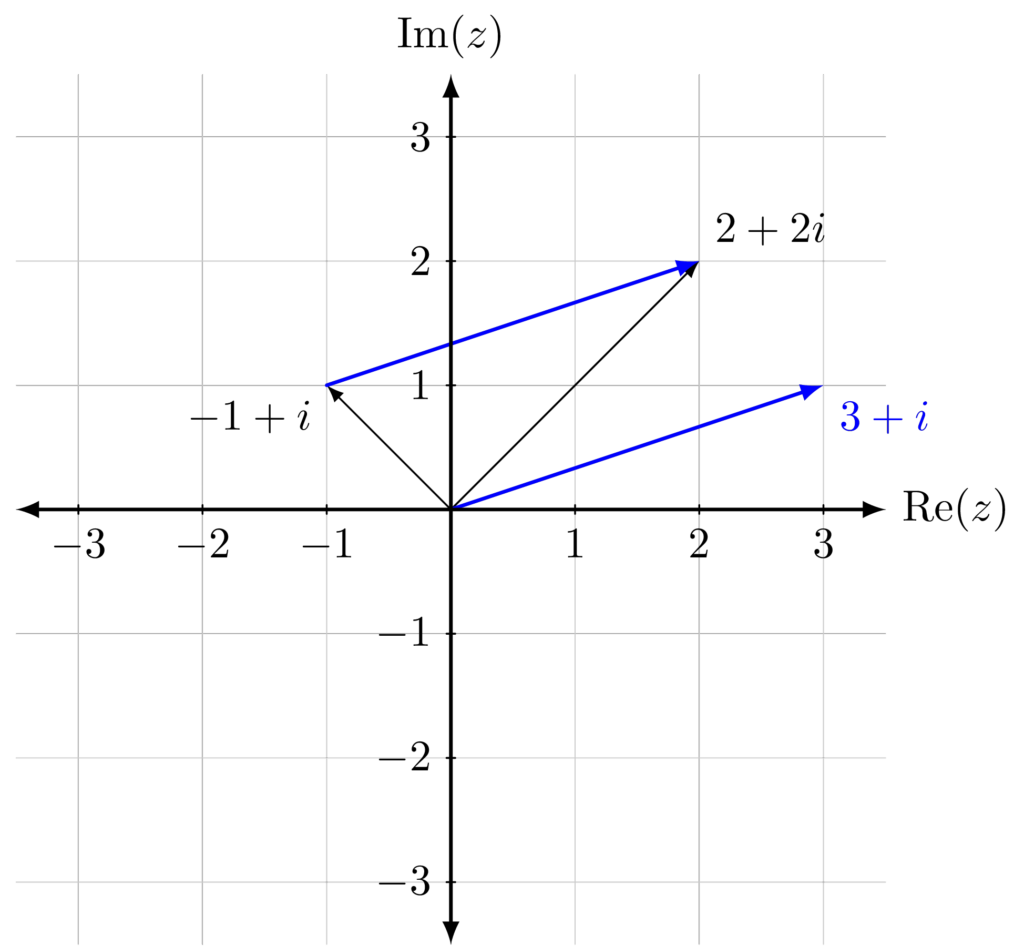
Another way of understanding \(z-w\) is that it is the vector from the point \(w\) to the point \(z\). We can therefore interpret \(|z-w|\) as the distance from the point \(z\) to point \(w\).
Example. Let \(z=(2+2i)\) and \(w=-1+i\) as in the previous example. We can see that the vector from the point represented by \(-1+i\) to the point represented by \(2+2i\) is actually the vector \(3+i\) (it has the same magnitude and direction, even though it doesn’t start at the origin). We can find the distance between \(z\) and \(w\) by evaluating $$|z-w| = \sqrt{1^2+3^2}=\sqrt{10}.$$
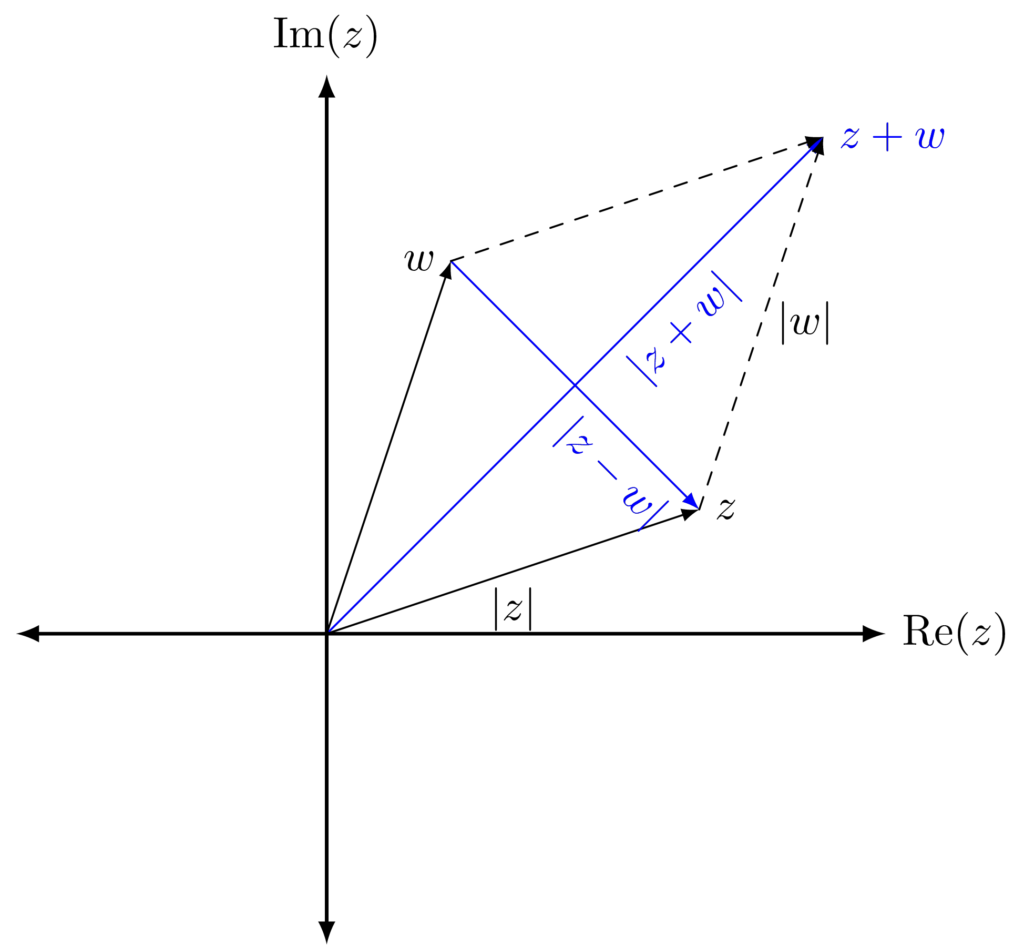
Worked exercise. Show algebrically that $$|z+w|^2+|z-w|^2=2(|z|^2+|w|^2).$$ What does this mean geometrically?
Solution. The algebraic exercise is left to the reader. Geometrically, we can see that we form a parallelogram when we depict \(z\), \(w\) and \(z+w\) on the complex plane, where \(z-w\) and \(z+w\) are the diagonals. \(2(|z|^2+|w|^2)\) represents the sum of the squares of the sides, and \(|z+w|^2+|z-w|^2\) represents the sum of the squares of the diagonals. The identity shows that, in any parallelogram, the sum of the squares of the diagonals is equal to the sum of the squares of the sides.
Problems
- Subtract the second complex number from the first. Plot them as vectors on the complex plane.
- \(1+i\) and \(2+i\)
- \(3-i\) and \(4+i\)
- Find the distance between the two complex numbers on the complex plane.
- \(3+4i\) and \(-1-i\)
- \(-2-7i\) and \(-3-2i\)
- \(100+100i\) and \(-50+50i\)
- Show that the complex numbers \(-2-2i\), \(1-i\), \(2+2i\) and \(-1+i\) form a rhombus in the complex plane.
- Show algebrically that $$|z+w|^2+|z-w|^2=2(|z|^2+|w|^2).$$
- Let \(z_1\), \(z_2\) and \(z_3\) be complex numbers represented by the points \(A\), \(B\) and \(C\) on the complex plane.
- Write down the complex number representing the vectors \(\overrightarrow{AB}\) and \(\overrightarrow{AC}\).
- Let \(D\) be a point on the complex plane such that \(ABDC\) is a parallogram. Show that the complex number which represents \(D\) is \(z_2+z_3-z_1\).