Polar form of a complex number
You can express every complex number in terms of its modulus and argument. Taking a complex number \(z = x+yi\), we let \(r\) be the modulus of \(z\) and \(\theta\) be an argument of \(z\).
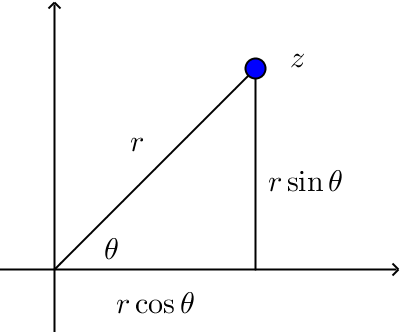
Using trigonometry, we find that \(x = r \cos \theta\) and \(y = r \sin \theta\). Thus we can write $$ z = r \cos \theta + ir \sin \theta = r( \cos{\theta} + i \sin{\theta}).$$
This can be abbreviated as $r \text{cis}{\theta}$, and is referred to as the polar form of a complex number.
Example. The complex number \(1+i\) has modulus \(\sqrt{2}\) and principal argument \(\frac{\pi}{4}\), so its polar form is $$ 1+i = \sqrt{2} \left( \cos\left(\frac{\pi}{4}\right) + i \sin\left(\frac{\pi}{4}\right) \right).$$
Argument properties
With this in mind, we have a couple of properties relating to arguments $$\begin{align*}
\arg(zw) &= \arg(z) + \arg(w) \\
\arg\left( \frac{z}{w}\right) &= \arg(z)-\arg(w).
\end{align*}$$
Let us prove the first one.
Proof. Let \(z = r_1 (\cos{\theta_1} + i \sin{\theta_1})\) and \(w = r_2 (\cos{\theta_2} + i \sin{\theta_2})\). So we have \(\arg(z) + \arg(w) = \theta_1 + \theta_2\). We want to show that \( \arg(zw) = \theta_1 + \theta_2\). We have $$\begin{align*}
zw &= r_1 r_2 (\cos{\theta_1} + i \sin{\theta_1})(\cos{\theta_2} + i \sin{\theta_2}) \\
&= r_1 r_2 ( \cos{\theta_1} \cos{\theta_2} – \sin{\theta_1}\sin{\theta_2} + i(\sin{\theta_1}\cos{\theta_2} + \cos{\theta_1} \sin{\theta_2})) \\
&= r_1 r_2 ( \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2)),
\end{align*}$$
making use of the compound angle formula in the last line. We can see that the argument of \(zw\) is indeed \(\theta_1+\theta_2\).
Problems
- Find the polar form of the following complex numbers.
- \( \sqrt{3}+i\)
- \(\sqrt{3}-i\)
- \(-\sqrt{3}+i\)
- \(-\sqrt{3}-i\)
- \(-2-2\sqrt{3}i\)
- \(-4+4i\)
- Prove that for complex \(z,w\), we have \(\arg\left( \frac{z}{w}\right) = \arg(z)-\arg(w)\).